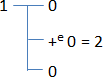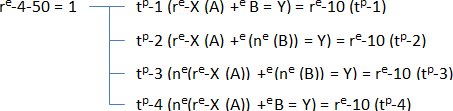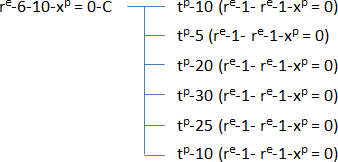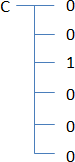
Circular mathematics

The context of the birth of circular mathematics began when the researcher has considered the development of the theory of evolution II (in the book “Physics of Angels”). This theory was developed to find a form of hierarchy in mathematical rather than promoting equality as usual in mathematics. The mathematical concept of hierarchy is an inequality that can apply dynamic changes in the value of numbers.

Since the theory of evolution II, the circular mathematics was studied to develop a graphics software, and also the researcher looks at the opportunity to innovate in many areas in mathematics, physics, and computer science.

We will see from this document several drafts on the circular mathematics, among other development in the new formulas, new operators and new rules in mathematics.

To create a hierarchy, we must create an inequality, so the unit should not be used to create the values of the numbers. To create the value of numbers, we use a tabloid that sets the value of the hierarchical numbers so as to allow the value of each number can be changed during operation in a formula. This means that the tabloid used to initialize the value of the numbers before the use of the formula.

Second aspect, the numbers of hierarchy exists if the numbers are unequal compared to the unit. But of course, even if we used the values of floating point numbers, it is nonetheless the unit becomes smaller and we use the unit in the end. But we should not use unit, even if it is smaller. This forms a margin of space between each number that is included in the value of the number, but not exactly as you can see now. The value becomes composed. A composed value is not an index or an address on a line, it is a value that is typical to the number itself. For example, for a hierarchical number, it does not start at 0, but between two symbols, or 2 sub-indices.

To create the value of a hierarchical number, for example, use “1.02” and “2.64”. These 2 terminals form a range, but it is not the difference between the terminals which forms the value is what it would take to paste the following hierarchical number that also has 2 terminals. The terminals are there to create an impossibility to stick hierarchical 2 numbers together. So, the terminals, unlike a unit, do not give unit value, they outpace hierarchical numbers unevenly. And the value of the hierarchical number is within these limits. For another hierarchical number, the terminals should not form a unit that is like another hierarchical number.

In addition, not only the terminals of a number are contactable with the terminals of another number, we use a variable “space” which defines the space occupied by the value of the number. The space is not used to redefine terminals, space is what creates inequality between each hierarchical number in their terminal. Since in reality the space is the variable that controls the convertibility of the terminals to make the values of inconvertible hierarchical numbers.

This is the hierarchy, the values of numbers are not comparable to this point, but the fact remains that it is logical to know which number is more than another. Since the hierarchical numbers are not indices, they have depth, then it is said that the depth creates hierarchical levels.

Operator “ +^e ”:

The “ +^e ” operator is used for concatenation or subtraction of space in a hierarchical number. For example, since the terminals of a hierarchical number are defined independently of the variable “space” of the hierarchical number, it forms a space for each unit between terminals, so we can decide to manipulate space contained in the variable space. To do this, for example, if we use the formula “ 1 +^e 1 ”, this does not give 2, this will cut 2 times the space in the hierarchy number “1”.

Operator "=":

Where is the cut space of a formula? It can be assigned to a variable. For example, if we add the “=” operator, it means that we do an assignment in a formula. For example, “ 1 +^e 1 = 2 ” means that we subtract two spaces to the hierarchical number “1” to give the hierarchical number “2”.

Symbol “0”:

We could create another example, “ 1 +^e 0 = 2 ”: in this example, “0” is not used as hierarchical number, but as an entity in a formula symbolizing in this case that the operator “ +^e ” applies only in hierarchical number “1” (the first polynomial of the formula).

In the formula “ 1 +^e 0^e = 2 ”, the “ 0^e ” means that one affects to 2 an original space from the hierarchical number “1”. This is useful when making operations with repetitive values.

Symbol “ , ” (comma):

If we write “ 1 +^e 1 = x,2 ”, this means that two spaces are assigned to the variable “x” and “2”. The decimal symbol used to duplicate an operation on several variables. For example, we could write “ 1,0^e +^e 0 = 2 ”, it means the same as “ 1 +^e 0^e = 2 ” (see the previous paragraph). In the context in which we use the point in “ 1,0^e +^e 0 = 2 ”, we duplicate the application of operator “ +^e ” on the second term (after the comma). So we could write a series of hierarchical numbers “ 1,1,1,2,3,4 +^e 0 = 2 ”.

Operator “ +ⁱ ” (concatenation index):

As in ordinary mathematics, the operator “ +ⁱ ” can be used for equivalence but not only serves this in circular mathematics. First “ +ⁱ ” is simultaneously the “ + ” and “ - ” depending on how it is used. For example, in the formula “ 1 +ⁱ 1 ”, it means that we replace the hierarchical number 1 in the hierarchical number 1. So “ 1 +ⁱ 1 = 2 ” is equivalent to “ 1 +ⁱ 0 = 2 ” or “ 1 +ⁱ 2 ” and actually means that we replace the value of the hierarchical number 2 by the value of the hierarchical number 1.

For the equivalent of “ 1 + 1 = 2 ” in ordinary mathematics, so that it gives 2 times the number 1, we must use the “ +ⁱ ” operator in this way: “ 1,0^e +ⁱ 0 = 2 ”.

As said, we also use the “ +ⁱ ” operator to the equivalent of a subtraction. In the formula “ 1 +ⁱ 0 = 2 ”, it means that we replace the value of the hierarchical number “2” by the line number “1”, so there would be a subtraction if for example the value of the hierarchical number 2 was higher the value of the hierarchical number 1 before applying the formula.

Operator “ b⁺ ”

This operator is used to check the bounds. By default, only the reference bound can be changed in formulas, so the upper bound, but we'll see how affected the lower bound. In a formula, if we write “ 1 b⁺ 1.0 ”, this affects adding 1.0 to the upper bound of the hierarchical number 1. Note: the values assigned to the bounds must always be decimal numbers (separated by a period not be coincident with the comma symbol). If we write the formula “ 1 b⁺ 0 = 2 ”, it means that we replace the bounds of the hierarchical number 2 by the bounds of the hierarchical number 1. If we write the formula “ 1,2 b⁺ 0 = 3 ”, this means that we replace the bounds of the hierarchical number 3 by concatenating the upper bounds of hierarchical numbers 1 and 2. To assign the lower bound, we must use the symbol “0” after the “ = ” operator. So, in the formula “ 1 b⁺ 1.0 = 0 ”, it means that one adds 1.0 to the lower bound of the hierarchical number 1. The equivalent is written as “ 1 b⁺ 1.0 = 1,0 ” which means the same thing. We could also write:

“ 1 b⁺ 1.0 = 2,0 ”: means that we replace the lower bound of the hierarchical number two by the concatenation of the upper bound of the hierarchical number 1 and 1.0;

“ 1,0 b⁺ 1.0 = 2,0 ”: means that we replace the lower bound of the hierarchical number two by the concatenation of the lower bound of the hierarchical number 1 and 1.0;

“ 1,2,3,0 b⁺ = 2,0 ”: means that we replace the lower bound of the hierarchical number 2 by concatenating the lower bound of line numbers 1, 2 and 3.

Subtracting the value of a bound will be explained later. This is very different because we do not want to be negative bound. In addition, it is noted that allocation of a higher value to the lower bound as the upper bound of product opposite directions, we will see the utility further.

Operator “ r^e ” and symbol “ - ”:

The operator “ re ” allows to repeat a space, and it is attached to the symbol “ - ” which is used to attach a value to an operator. For example, in the formula “ 1 r^e-1 = 1 ”, we assign a space (repeated 1 time) to the hierarchical number 1 from the same number: it subtracts space since the operator “ +^e ” not allowed that implicitly unless we would have written “ 1 +^e 0 = 1 ”, but this has no effect on the space if bounds form one unit. Note: with this operator, the bounds are redefined in the formula “ 1 r^e-1 = 1 ”, that is how we can also decrease the bounds. Explicitly, the initial value of a lower bound is set at first, but can be increased or reset to the value of a bound of another hierarchical number or needing initial value with an operator we shall see below.

If later we want to create a logical sequence such as numbers of ordinary mathematics, then we write “ 1,0 b⁺ = 2,0 ”, “ 1 b⁺ = 2 ”, and “ 1 r^e-2 = 2 ”. Obviously, we could also create a number of ordinary result without playing on space, but the bounds.

The operator “ r^e ” can also be used without the symbol “ - ”. With the phrase “ r^e 0 = 1 ”, we remove the hierarchical number 1: with circular mathematics, we can remove entities. With the formula “ r^e 2 = 1 ”, we replace the hierarchical number 1 by the hierarchical number 2. With the formula “ r^e 1,2 = 1 ”, we perform a fusion hierarchical numbers 1 and 2. With the formula “ 0 r^e 2 = 1 ”, we recreate the entity 1 taking as a basis the hierarchical number 2. with the formula “ 1 r^e 2 = 3 ”, we replace the hierarchical number 3 by the hierarchical number 2 on condition that the hierarchical number 1 is included in the hierarchical number 2: the condition will be very useful, we will see a little later in the document.

Operator “ x^p ”:

The “ x^p ” operator is the art operator of the circular mathematics (the x and p means multiple means sharing). With this operator you can change the hierarchical numbers in use as multiple mode to create composite numbers or to create composite functions.

In the formula “ 1 x^p 1 ”, the space is not cut, but it is multiplied. If you write “ 1 x^p 0 = 2 ” you multiply the space taken in the hierarchical number 1 to the hierarchical number 2 for all units between the bounds of hierarchical number 2.

In the formula “ 0 x^p 0 = 2 ”, the hierarchical number exists but contains 0 space in the units between bounds.

In the formula “ 1 x^p-3 = 0 ”, that create three floating spaces from the hierarchical number 1. This is how you can have space in the circular mathematics without numbers attached to these spaces . We will see later how useful this.

In the formula “ x^p-3 = 0 ”, it creates void spaces that are still spaces but which have an attractive value. So we can dose the attraction between two numbers as follows “ x^p-1 = 1,2,3 ”: this has the effect of creating an attraction of 1 null space between the numbersè 1 and 2, and between 2 and 3 . This forms a hierarchical composite number 123.

If we write “ 1 x^p-4 = 1,2 ”, this gives 4 spaces of the hierarchical number 1 between hierarchical numbers 1 and 2. This is not the opposite of attraction, only they distanced in this way and so this forms a hierarchical composite number 12.

As this had not been explained before, we now approach the subject of ascension of hazard. In circular mathematics, there is a benefit, the results are unique. This means that in physics, we come to explain certain phenomena through the circular mathematics. But we will not discuss all that this can cause, only part that we will see throughout this document.

For there to be ascension of hazard, every time we use a space, this space is subtracted of the hierarchical number. But the hierarchical number is endless and not exhausted really, since the remaining space is always shared between bounds, so space is infinite. However, the value of the space changes with each use.

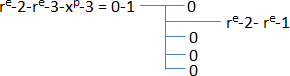
An exception: if there is only one space between bounds, so space becomes void if used, but the hierarchical number still exists. To recreate the space, simply use the formula “ re-2-50 = 1 ”. In physics this is called an application of the concept of space recreated which is a concept explained in the "The keys of physics." In this formula, we create two repeating units of 50 spaces in the hierarchical number 1.

To begin with complex formulas, we will discuss what is called the composed space. The composed space is how we will achieve concrete results with the circular mathematics. First, are starting with the following formula:

In this formula we use the “ - ” symbol. This symbol is the implementation of a first branch of a hierarchy. The formula shows that simple hierarchies. The explanation of this formula is as follows: “ x^p-3 = 0 ” creates three floating spaces, “ r^e-2 ” creates two repetitions, and “ -1 ” means to add these two repetitions of three floating spaces at the hierarchical number 1. This means that the space is composed in this hierarchical number with 3 divisions per unit in a floating dimension. So we can then use the hierarchy symbol three branches for handling this hierarchical number:

In this new formula, we subtract 1 space at the second hierarchical level of the hierarchical number 1 to move it to the hierarchical number 2. Obviously, since the space is floating, so it retains its hierarchical position (second) initial the number 1 when it is placed in the number two.

The role of the floating space is to make different the value of the first space. This differentiation adds to the space a first multiplication of the space in a dimension which can be multiple. We can use multiple values in a single hierarchical number, which makes it searchable. Exploration is the same key of the circular mathematics. In the universe, the space acts to make the physical environment explorable things. Exploration within a number enables it to have a depth, so can contain something rather than being a simple index like numbers of ordinary mathematics. Here, the number is more than a symbol for computing, it is a source of values. Let us look at the study of the source of values.

The operator “ = ” can be placed before the hierarchical number having several hierarchical levels:

This new formula creates what can be called hierarchical amplitude. In this context, the hierarchy is developed within the same second hierarchical level of the hierarchical numbers 1 and 2.

We can see now that there is indeed the possibility to create hierarchical numbers from simple formula in circular mathematics.

We have seen that the variable space existed in reality this is not the only element, there are other hierarchical factors. Circular mathematics is really well thought out to create physical models. First, we have previously observed the behavior of operators on space. These are the same operators to be used for other elements that are also hierarchical factors.

The other factor that we will approach has been called “reverse hierarchy”. This factor is composed of a memory, so we will approach the management of the memory with the circular mathematics.

The hierarchy enables us to save the space inside bounds. So, we will use the same kind of principle except create hierarchical positions in what can be called a hierarchical Cartesian plan.

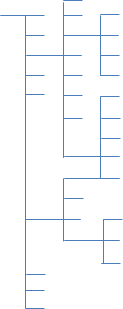
In simple hierarchy (or traditional) shown in Figure 1, we understand this hierarchical diagram. A memory may be created based on the extended position. This kind of memory is the one typically found in all systems using ordinary mathematics. But now you will see in Figure 2 that the hierarchical chart can be developed according to the position of the sub-branch and not of the upper branch.

In the hierarchical number, we can define the bounds and also shift the space inside of these bounds. This means that it helps to define a memory using all hierarchical positions, so there is no exclusivity. We then get a memory from the concept of the inverse hierarchy.

Figure 2 shows a diagram of the inverse hierarchy. It should be noted that there is a branch embarks on another branch, this is the main reason why we call the inverse hierarchy. First, it does not interfere at the mathematical since in fact, the branches of highest hierarchical level do not touch. This serves to create a point “O” (circle) in the hierarchy. We see the utility points “O” below.

The following formula is used to create the first inverse hierarchical level:

This formula was used to create the following hierarchy chart:

This formula can be explained as follows: with the term “ x^p-3 = 0 ” we create three floating spaces within the term “ r^e-2-r^e-3 ” (meaning the repetition of creation of 2 sections, one of 2 repetitions and the other 3), all of it assigned to the hierarchical variable 1 (after the “ = ”, there is “ -1 ”). If we had written “ r^e-2-r^e-3-r^e-1-x^p-3-x^p-4 = 0-1 ” in the first term of the formula, we would have obtained the following inverse hierarchical diagram (1st level):

The inverse hierarchy can also mingle with space, such as in the formula “ r^e-2-50-r^e-3-x^p-3 = 0-1 ”, the term “ r^e-2-50 ” creates 2 units of 50 spaces. It is also possible to customize each unit with a term “ r^e-2-50-25 ”. It is noted that the space omitted from the formula leads we use the latest customization of the space to create value, so “ r^e-4-50-25-75 ” will ensure that the last 2 units are in 75 spaces.

We will now see how to create a point “O” (circle) in the reverse hierarchy diagram. To get there, we must address the third factor. Earlier we discussed the factors “space” and “memory” (inverse hierarchy). The third factor is time.

The time is at the origin a mechanical synchronization with ordinary mathematics. However, the time factor with circular mathematical also called “inverse time”. The inverse time is somehow to signify the past, present and future; therefore, it is the time line. But the inverse also determines distortions in time, and to catch up with the time having distortion. But more specifically, we do not play to create distortions in time, these distortions are created by themselves with the circular mathematical and time factor.

A new operator is used to time, “ tp ” operator: the abbreviation “t” means "time" and “p” means "sharing". The operator uses such as “ t^p-50 = 1-r^e-0 ”. In this formula “ 1 ” is the hierarchical number 1 which is assigned to the result of the operator “ = ”, “ -r^e-0 ” means for all units of the hierarchical number 1, and “ t^p-50 ” means that the 50 per unit time is assigned to the hierarchical number 1. If we had written “ t^p-50 = 1-r^e-2 ”, it means that we assign the 50 times in the 2 first units of the hierarchical number 1. If we had written “ t^p-50-25 = 1-r^e-2-r^e-3 ”, it means that we assign the 50 times in the 2 first units and 25 times in the last three.

The time lines are always read in the same time in a hierarchical diagram of a number. So, if it is set 50 times in many places, they are at the same time, etc. A time having less than one means that it is the past of the other. The same time is also a way to call this point "O" (circle) that we mentioned earlier. It is possible to set unique time automatically if desired. For example, if we place the hierarchical number to “ t^p ” that way “ 1 t^p 0 = 2-r^e-0 ”. This last formula means that the time of the first unit (default) will be cut off as space each time the unit is assigned to the hierarchical number 2. Since time is united (point “O”) by the same number, all units of the point “O” are readjusted according to the time remaining when time is subtracted. It may be that the point “O” merge if the same number when times of retrenchment operations are performed.

Reading the time is also used to join the units. With the point “O”, we can join multiple units simultaneously. The operations on time are performed as follows. With the phrase “ r^e-1-100 = 1 t^p-50 ”, it means that all units having 50 times in the hierarchical number 1 shall be replaced by their space 100. With the phrase “ r^e-2 = 1 t^p-50 ” this means that all units having 50 times in the hierarchical number 1 will be sees added an additional unit, doubly units that keep the same settings.

Other operations can be performed with time as assigning a new value to a bound: formula “ b⁺-1.25 = 1 t^p-50 ”, which assigns the value 1.25 to the current value of the upper bound of all hierarchical branches having at least one time to 50. For the assignment of a lower bound, this is done with the formula “ b⁺-1.25 = 1,0 t^p-50 ” we added “ ,0 ”.

To make different possible operating, remember that you can use “ 0^exponent ” which means “original value” in most cases, as in the formula “ 1 t^p 0^t = 2-r^e-0 ”. But we can also use for bounds, as in the formula “ b⁺-0.1 = 1,0^b t^p-50 ” which means to preserve the value of the original lower bound of the hierarchical number 1, but offset by 1 unit every other units, allowing the addition unit in early hierarchical branch, that we could not do with “ r^e-2 = 1 t^p-50 ”.

To understand and perceive the usefulness of circular mathematics, we must learn to create composite functions. A composite function can make the link between theory and practice. Let's start right now to see how we can make composite functions and then see their application in reality.

To create composite functions, we usually use the same operators as those seen previously, except that they will be used in a function context, so to allow imbrications of instructions.

Since we used the space as a variable, then that variable will be contained in brackets “(” and “)”, and may contain formulas and instructions, this is the space. The hierarchical chart will always be used for the composite functions, and the time is also a reference to a portion of a function. In addition, the time can be mutated to variables.

Function composed:

1 (t^p-50) +^e 2 (t^p-100) = 3

In this function, it means that we are all time units 50 contained in the hierarchical number 1 with all the time units 100 contained in the hierarchy number 2, then assign to the hierarchical number 3.

Function composed:

r^e-2 (1 t^p-50) = 2

In this function, we retrieve 2 time units 50 contained in the hierarchical number 1 to assign the hierarchical number 2.

Function composed:

r^e-2 (1 (0^e)) = 2

In this function, we repeat 2 times the content of the parenthesis (space) which itself contains the extraction of a space at original value of the hierarchical number 1, and this space is then multiplied 2 times assigned to the hierarchical number 2.

Function composed:

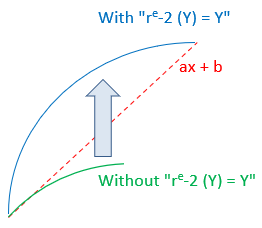
r^e-X (A)) +^e B = Y

This function is equivalent to the ordinary mathematical function y = ax + b. The variables are always written in capital letter not to be confused with operators. A variable is equivalent to a space. We could replace these variables by other formulas of the circular mathematics.

Function composed:

t^p-1 (r^e-2-30-40-t^p-2-3 = 1) = r^e-2 (t^p-1) = 2

This feature is explained as follows: The term “ (r^e-2-30-40-t^p-2-3 = 1) ” means that we assign the hierarchical number 1 of 2 units with a space of 30 and 40, with the time 2 and 3; the term “ t^p-1 (…) ” means that we keep a reference to time 1; the term “ = r^e-2 (t^p-1) ” means that we repeat two times the reference on beat 1; and the last word “ = 2 ” means that we affect the two repetitions of the reference to the time 1 to the hierarchical variable 2.

Operator “ f^x ” (fracture, break):

This new “ f^x ” operator allows to break the terms of functions, thus breaking space somehow. It is used as follows: in the formula “ (1 t^p-50) f^x-2 ”, this means that the time 50 in the hierarchical number 1 is fractured into two units with their space also fractured by 2, but they keep the time 50. Note: time never fracture.

Considering that we have the time factor, we can synchronize functions within a hierarchical chart. Here is a function that synchronizes multiple formulas.

In this formula, the new operator “ ne ” means “negation”, it transforms an operation in withdraw, the equivalent to create negative values, except that it applies only in the space factor. For example, when converting a withdrawal space and that there is only one unit in the hierarchy number, so the lower bound obtains a value above the upper bound. So, a negative value can be in the hierarchy diagram that if only the lower bound is superior to the upper bound: therefore the opposite direction to space.

In the previous function, since it is the variables A, X and B, then the formula is waiting for filling the original values of these variables. The function executes a diamond shape, although at this stage we have not yet seen the geometric forms, this is a simple geometric shape in this context.

When we uses the above formula, we must do it this way: “ 1 (1.0 = A-0^e, 0.0 = X-0^e +^e 1.0, 0.0 = B-0^e) ”. In this formula, we call the hierarchy number 1 which contains multiple functions, and we ask that assigned to the variable “A” value “1.0” and so on for other variables, then we specify for the variable X that this value must be increased to “1.0” at each time it is invoked (except for the first time whose initial value is running). “ 0^e ” symbolizes the variables retain their original value every time they are called.

In addition, the circular mathematics has the advantage to use the same function to create several possible outcomes. In the latter case, we created a diamond except that we can also create a circle or spiral. For example, if we call the hierarchy number 1 with the formula “ 1 (1.0 = A, 0.0 = X-0^e +^e 1.0, 0.0 = B-0^e, r^e-2 (Y) = Y) ”. In this new call to the hierarchical number 1, we removed "0^e " for the allocation of variable A (causing an entrenchment of space, assume here that we initialized this variable with at least 2 units), and we added a Y assignment of his double, creating a circle. In this context, this circle is not yet perfect since it would play with some parameters such as the duration of the function that is set to “10” in this context, but the “10” could be replaced by a variable which give us another room for maneuver with the function. We discuss later the graphical functions.

Originally, the Cartesian plan comes from the card manufacturing. In a more sophisticated context, we can know for instance that the earth is not flat, changing the plan of a card. For impeccable details, we need a more advanced version of the Cartesian plan. Something both which can also map the universe.

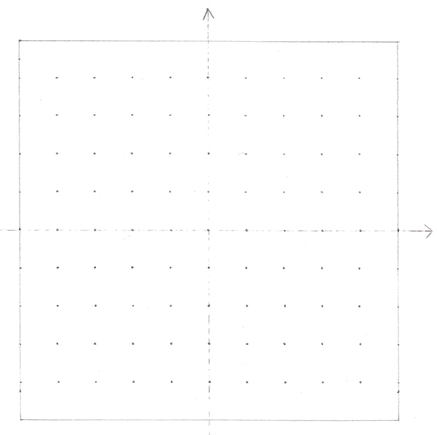
In Figure 3, this hierarchical Cartesian plan is colored in certain places to show you the shape of the Cartesian plan. First, there is a single axis (the colored part in red). The center is never used in the hierarchical coordinate grid for the simple reason that the center is not the empty point on the graph, the center is the circle and there are several centers. The colored parts in yellow, blue and orange are hierarchical diagrams that can form inside the hierarchical Cartesian plan: it is also how we will use the hierarchical Cartesian plan.

As observed, the Cartesian plan has not actually the same utility that an ancient Cartesian plan. First, the axis can also flex in a context of three dimensions. Unlike the old Cartesian plan, the axis can take the shape of a curve, vertical or horizontal. This hierarchical Cartesian plan is designed for circular mathematics, and cannot be used other than the circular mathematics.

Hierarchical Cartesian plan has several advantages over the old Cartesian plan. First the context of space here is not determined by the position of a point in the graph, space is typically manageable by the hierarchical numbers and variables. What determines the number in a hierarchical amount of space / volume used. But, here's the ultimate benefit of the Cartesian plan is that it allows you to reuse the same space since space is accessible from various points in the graph, so the hierarchical Cartesian plan allows to use space according the concept of the space recreated. The space recreated is as was defined in the document “The Keys of physics.” As we can now have shapes with recreated space surfaces, it is a mathematical innovation.

Here is how we use the hierarchical coordinate grid. First, we are sailing in the main axis (red colored part in Figure 3) with time. As the time can never equal 0, then the first time is the first circle to the center of the graph, and other circles are other times. Since time does not equal 0, then at 0 there is no time, so within the first circle in the center is not used.

In addition, time is also used to gather several hierarchical branches, which is a further development of the concept of the recreated space. Such time to the point “O” in a hierarchical number is represented on the graph as circles, therefore not depending on ordinary Cartesian position. The different axes in the graph can be reached from the first axis (red colored portion) with respect to another hierarchical number. This is called “the time that contains itself”. That this definition, objects (or hierarchical numbers) are positioned according to their time to contain them. So, an object if placed alone, always begins to exist on the main axis.

To control the axis we use, we obviously use hierarchical numbers. At the same hierarchical number, structure, changes the time structure of hierarchical coordinate grid. This means that the hierarchical Cartesian plan, the order is given by the hierarchical numbers used and not by the logic in the chart as a sequence of logical number. So, there is no real of following logic of numbers. The logic is not in the following, it is in the interpretation of hierarchical numbers.

As for example, in Figure 4, we represent a hierarchical number by the main branch in the first place, the time “ t^p ” of the first unit. It is noted that the first position will depend on the Cartesian plan the graphic and time. According to the graph, starting with the first unit we calculate from this first unit. So, on the first circle of the graph, there are 6 time, on the second, there are 12 other time, and so on, so the position “50”, for example, should be located on the fourth circle. But this position is the default position. Obviously, we can play with the definition of time inside the hierarchical Cartesian plan.

To edit and manage time of hierarchical positions of the Cartesian plan, we use in fact a hierarchical number to manage the Cartesian plan.

In the formula above, we configure the first hierarchical level of the variable C (selected for “Cartesian”). “ x^p ” is only to leave free the number of hierarchical levels to be created. We can see that the recreated space phenomenon can occur even with the definition of Cartesian plan. For example, if we define with “ r^e ” in the second hierarchical level 2 more repetitions in some places, so we make a hierarchical Cartesian plan that is not equal everywhere as in Figure 4.

In addition, when the time is set, then the default time is not the same as it was originally. This means that the time of a lower branch therefore depends on the higher entity. In the formula above, since “ t^p-10 ” is defined, this results in lower-level branches starting to “ t^p-11 ” by default. The Cartesian graph can have several times the same time in several places, creating “O” dots (circle). So, to understand, a circle is a time in the graph, which also allows to unite several points at once. Depending on how the times will be defined in the graph, then even if the circles follow each other physically, time will not have the same order.

To continue in formulas, a little more complex, here is a formula that positions the hierarchical number 1 in variable C (“C” for “Cartesian”):

In this formula, it should be noted that as soon as “C” is defined, we do not need to redefine it, “1” is alone assuming that it is already defined. When 1 is placed there, it replaces all the old arrangements of the graph with this hierarchical branch. To avoid this, add “ -0 ” after the 1, and the Cartesian plan keeps by inserting the hierarchical number 1. The hierarchical number 1 is then in another dimension of the Cartesian plan. We know now how to create dimensions at the Cartesian plan. Let us remember that a variable or hierarchical number is a gateway to a new dimension if there is “ -0 ” in front.

We have seen one of the wonders of circular mathematics is that numbers can be inserted into other numbers. To put multiple numbers in the same hierarchical branch, use the symbol " , " like that “ 1-0, 2-0 ". The variables or hierarchical numbers can be inserted in more than one place in a Cartesian plan or within the same number or variable. To remove them, use “ n^e (1-0.2-0) ”. We can also destroy a hierarchical branch with “ n^e (0) ” apply on the branch that we want to remove. Now you've learned how to manage a hierarchical Cartesian plan (via a hierarchical variable).

The hierarchical Cartesian plan is used within other forms of Cartesian plan of ordinary mathematics. The hierarchical Cartesian plan is a point on the other Cartesian graphs. It is said that everything is connected in the universe, and well with a combination of ordinary mathematics and hierarchical mathematics we all manage to connect together.

The concept of using the Cartesian hierarchical plan as a point is rewarding. First, we can create complex results with circular mathematics, which enriches the task of ordinary mathematics. So, here's what a combination of the 2 mathematics can do.

First, a point is achievable with the hierarchical Cartesian plan since the tips join inside the concept of the graph because of the concept of the recreated space. This suggests that circular structures are made graphically. In addition, there is the 3D concept that defines several dimensions by merging several Cartesian plans using the management of hierarchical variables. This gives rise to multidimensional structures that we will call “spherical structures” that are achievable only with circular mathematics. In a way, we call these spherical structures as we call a dot.

Matrix Cartesian plans such as those used in ordinary mathematics are used to create divisible structures if used alone. The advantage of using it with circular mathematics will be to give a constructive character to mathematical models. A united structure has many more advantages both in terms of geometric shape conceptualization or other designs. The benefits will be presented to you as you go along.

First, if we have an indivisible structure, such as a hierarchical Cartesian point, this point solves problems at the limits of mathematical models, since this point is as we can say, an object, not just a index. The index is empty, while the dot is full. Then we will still use the ordinary Cartesian plan in the same form, but this time with points instead of segments. In a sense, Cartesian graphics with spherical structures are at the graphic resolution “atomic dot” that symbolizes “atomic point”, representing a finite structure with dots.

On a Cartesian plan without circular mathematics, the dots do not really exist since they are a divisible part in 2 or several. So now is the time to use circular mathematics to make a point, a real point. A point is an entity that can now store information, formulas and much more, structures, etc. We are not just working on a volume scale.

With the Cartesian "atomic dot" plan, the dot itself can move. Indeed, this is possible. Suppose that in a call to point P1 (hierarchical variable), we write this “ P1 (Y = P1-Y = P1-Y +^e 1.0 = P1-Y) ”: in this formula we make an assignment from Y (called) to P1-Y (which the position of the P1 point on the Y axis), and an assignment still to P1-Y with a double displacement of 1.0.

A dot, a hierarchical Cartesian plan, can contain several functions, and thus contain several curves on a Cartesian “atomic dot” graph. Thus, when a point moves, it also moves up to several curves on a Cartesian “atomic dot” plan. One point is also connected to another point with the term “ P1-P2 ” which simultaneously links 2 points together, P1 to P2. We can also move multiple points simultaneously with the call to the following function “ P1 (+^e P2, +^e P3, +^e P4, Y = P1-Y +^e P2-Y +^e P3-Y +^e P4-Y) ”, this affects the Y result for all P1 to P4 variables containing Y. We've added “ +^e P… ” the beginning of the opening of the parenthesis, this is not to be interpreted as independent variables. It is also the method of linking several points together permanently. If you want to break the link, just write the formula “ P1 (n^e (+^e P2)) ”.

The behavior of the dots in a Cartesian “atomic dowry” graph remains independent of each other, even if they are related.

The merging of points is another element that we will use. Fusion is an element used to create surfaces, for example, that can be full or have transparent parts. This can also be used to create shapes in form.

The fusion thus begins with the absorption of points. For example, the absorption of points is done by the following formula “ P1 +^e 0-(4.0 = X, 2.0 = Y) +^e 0-(5.0 = X, 2.0 = Y) = P1 ”. In this formula, the P1 defined point is merged with two other points. The symbols “ 0 ” and “ - ” are used to symbolize a floating dot on the Cartesian "atomic dot" plane. Within the P1 variable, access to the 3 points it includes is simultaneous. So, we could also in this way create width in a function. However, in order for these points to move at the same time as P1 in the event of a point shift, this must be stated as “ P1 (+^e 0-(4.0 = X, 2.0 = Y), …) ”. To remove a point merge “ P1 (n^e (+^e 0-(4.0 = X, 2.0 = Y))) ”.

It is interesting to note that a point may contain several points in the Cartesian “atomic dot” graph. It also allows you to create Cartesian graphics with a shape instead of the dot. For this to happen, let's use the following formula “ P1 = *0 ”. The symbol “ * ” symbolizes “for every point of.” To create a line of special dots “ P1 = *0-(2.0 = Y) ”. And apply to a formula such as y=ax+b : “ P1 = *0-(+^e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X +^e 1.0 = X, 1.0 = A, 0.0 = B, r^e-10 (re-A (X) +^e B = Y)) ”, that means that the variables X and Y starts at 0.0, for each call of X, X is increased by 1.0, and the function is repeated 10 times. It's worth noting that we've also included “ +^e 0-(*0 = X, *0 = Y) ” so that all points merge to P1 also move. If this had been omitted, the function would have kept the reference on the same merged points at P1.

We can also print a mosaic shape fused by its dots. For example, the following formula does so, “ P1 = *0-(+^e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X, r^e = *0) ” from the ordered origin of the Cartesian “atomic dot” graph. For a mosaic with shift “ P1 = *0-(+^e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X + 0.5 = X, r^e = *0) ”. This is how we can create all kinds of dot dies on an “atomic dot" Cartesian graph.

In addition, it is important to consider that we can link the entire point universe of an “atomic dot” Cartesian graph by having omitted “ +^e 0-(*0 = X, *0 = Y) ”.